There are several ways to find the perimeter of a rectangle through the dimensions of its sides, area, diagonal, or radius. If humanity had not learned to calculate this value, it would have been impossible to perform accurate calculations in construction, measure land plots, etc. Let’s consider the formulas that allow finding the perimeter of this figure, as well as examples of solving geometric problems using them.
Earlier we wrote – Global Warming: Truth and Myths, Causes and Consequences
Common Formulas
First, let’s recall that the perimeter is the sum of the lengths of the sides of a geometric figure. This value is one of the basic ones in mathematical calculations. It is denoted by the Latin letter P. Children become familiar with this value in elementary school. The ability to calculate the perimeter is a necessary condition during the compilation of the State Final Examination in primary schools in Europe.
A rectangle differs from other figures in that it is a quadrilateral with equal opposite sides, meaning both its lengths are equal, as are both its widths. This is fundamental when calculating its P.
How to Find the Perimeter of a Rectangle by Its Sides?
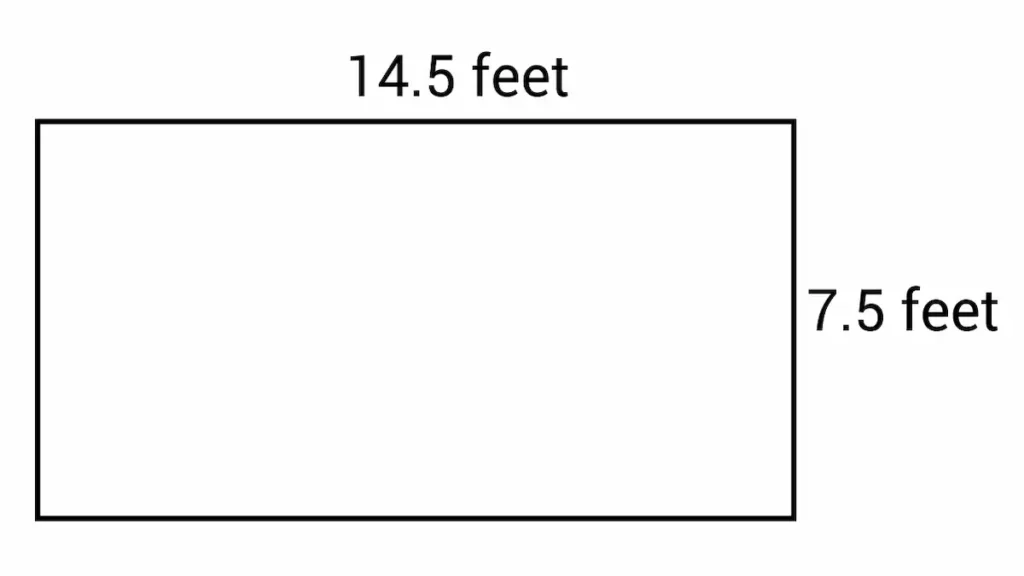
If the dimensions of the length and width of the rectangle are known, its perimeter can be found using the formula P = 2(a + b), where:
- P – perimeter;
- a – length;
- b – width.
This formula is the simplest way to calculate P. Students learn it in elementary school.
Calculations Using One Side and the Area
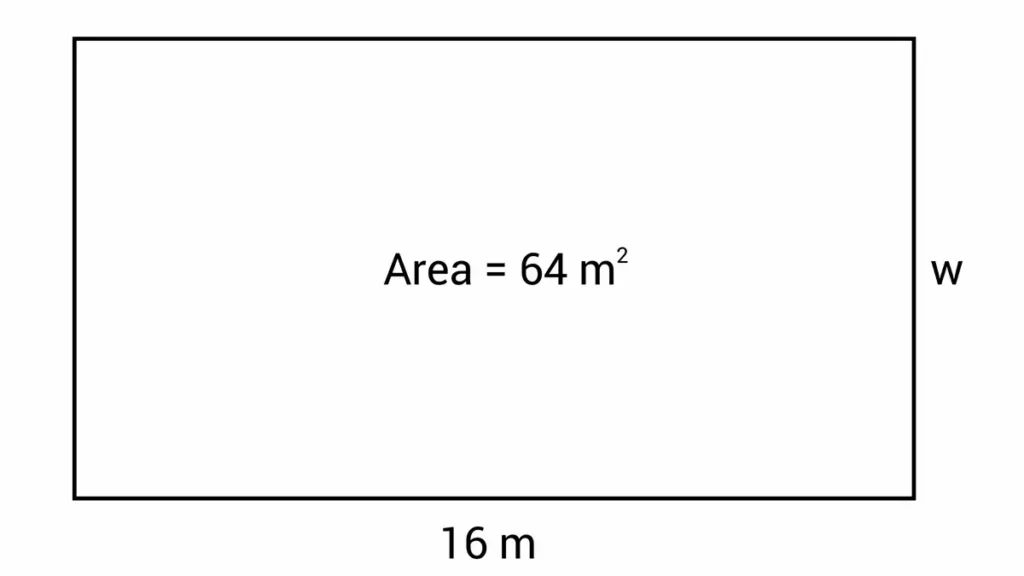
Now let’s consider how to find the P of a rectangle knowing its area and the size of any side. For this, the geometric formula P = 2(a + S / a) is used, where:
- P – sought perimeter;
- a – length;
- S – area.
How to Find the Perimeter of a Rectangle by Its Diagonal?
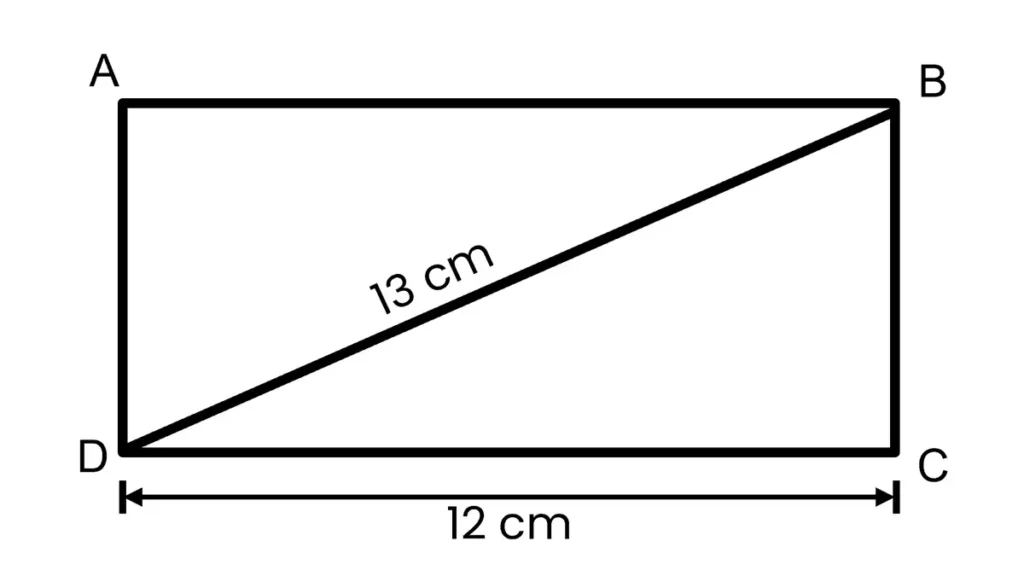
Calculations can also be performed when the length of the figure’s diagonal and any of its sides are known. In such cases, the formula P = 2(a + √(d² – a²)) is used, where:
- P – perimeter to be found;
- a – size of any side;
- d – length of the diagonal.
Formula Using the Radius of the Circumscribed Circle
Sometimes the question arises of how to find the perimeter of a rectangle if only one of its sides and the radius of the circumscribed circle are known. For this, the geometric formula
P = 2(a + √(4R² – a²)) is used, where:
- P – perimeter;
- a – side length;
- R – radius of the circumscribed circle.
Examples of Problem-Solving Using Formulas
To understand better how to find the perimeter of a rectangle, let’s look at examples of problem-solving using the above formulas. Solving such tasks will not only improve students’ performance but also positively influence their spatial thinking development.
Problem 1
Find the P of a rectangular figure if its length is 10 cm, and its width is 7 cm.
Since all sides of the rectangle are known, use the formula P = 2(a + b), where side a is 10 cm, and b is 7 cm.
Substitute the data and get P = 2(10 + 7); P = 2 * 17; P = 34.
Answer: 34 cm.
Problem 2
Calculate the P of a rectangle if it is known that one of its sides is 6 cm, and the other is 3 cm longer.
To find the required value, first determine the size of the unknown side: 6 + 3 = 9. Hence, the length is 9 cm.
Since we know the lengths of both sides of the rectangle, use the formula for finding the perimeter by its sides: P = 2(a + b).
Perform the calculations: P = 2(6 + 9); P = 2 * 15; P = 30.
Answer: 30 cm.
Problem 3
A rectangular pool has an area of 150 m². It is known that one of its sides is 10 m. Calculate the P of the pool.
Since we know the area and the length of one side of the rectangular pool, calculate its perimeter using the formula P = 2(a + S / a). Substitute the known values and get: P = 2(10 + 150 / 10); P = 2 (10 + 15); P = 2 * 25; P = 50.
So, the perimeter of the pool is 50 m.
Problem 4
There is a rectangular flowerbed with a side a, which is 6 m. It is known that the diagonal d is 10 m. What is the P of this flowerbed?
We know the diagonal and one side of the flowerbed, so to solve the problem, we need to use the formula P = 2(a + √(d² – a²)). Substitute the available values and get: P = 2(6 + √(10² – 6²)). Perform the mathematical operations: P = 2(6 + √(100 – 36)) = 2(6 + √64) = 2(6 + 8) = 2 * 14 = 28.
Answer: P = 28 m.
Problem 5
In a rectangle, the radius of the circumscribed circle R is 5 cm. Calculate the P of the geometric figure if the length of its side a is 8 cm.
If we know the radius of the circumscribed circle and the side, then we need to find the perimeter using the formula P = 2(a + √(4R² – a²)). Solve the problem as follows: P = 2(8 + √(4 * 5² – 8²)) = 2(8 + √(4 * 25 – 64)) = 2(8 + √(100 – 64)) = 2(8 + √36) = 2(8 + 6) = 2 * 14 = 28.
So, the answer is 28 cm.
How to Find the Perimeter of a Rectangle: Video with Formula and Problem Solving
To better understand the methods of finding the perimeter, we suggest watching the following video from YouTube.
Frequently Asked Questions and Answers
To do this, you need to add up the lengths of all its sides. The resulting number will be the sought value.
You need to use the formula P = 2(a + S / a), where a means width and S is its area.
It is measured in standard units of length: cm, dm, m, km.
In all formulas and problems, it is denoted by the capital Latin letter P.
This skill can be useful when calculating the amount of building and finishing materials during construction and renovation. Also, the ability to calculate the perimeter is needed in land surveying, space planning, financial affairs, etc.