Розглянемо, як знайти площу квадрата кількома способами: за сторонами, діагоналлю, периметром, та при умові, що він вписаний в коло. Якщо використовувати прості формули, про які йде мова у статті, тоді не доведеться витрачати зайвий час на розрахунки площі цієї геометричної фігури.
Квадрат та його площа
Але перш ніж переходити до теми, як знайти площу квадрата, згадаємо, що це за фігура та в чому її особливості. Квадратом називається чотирикутник, в якому всі сторони рівні між собою та знаходяться під кутом 90 градусів один до одного.
Площа квадрата – це поверхня, яку він займає на площині. Вона обчислюється в см², дм², м² тощо та позначається літерою S.
Як знайти площу квадрата за допомогою геометричних формул
На уроках математики в середній школі діти вивчають різні способи, як знайти площу квадрата. Найпростіший з них – обчислити поверхню фігури через довжину її сторін. Для цього потрібно лише перемножити їх між собою. Отримане число й буде потрібним результатом.
Ми вже згадували, що у будь-якої квадратної фігури всі сторони мають однакову довжину. Якщо позначити їх через букву a, то формула знаходження S в цьому випадку матиме наступний вигляд: S = a * a, або S = a².
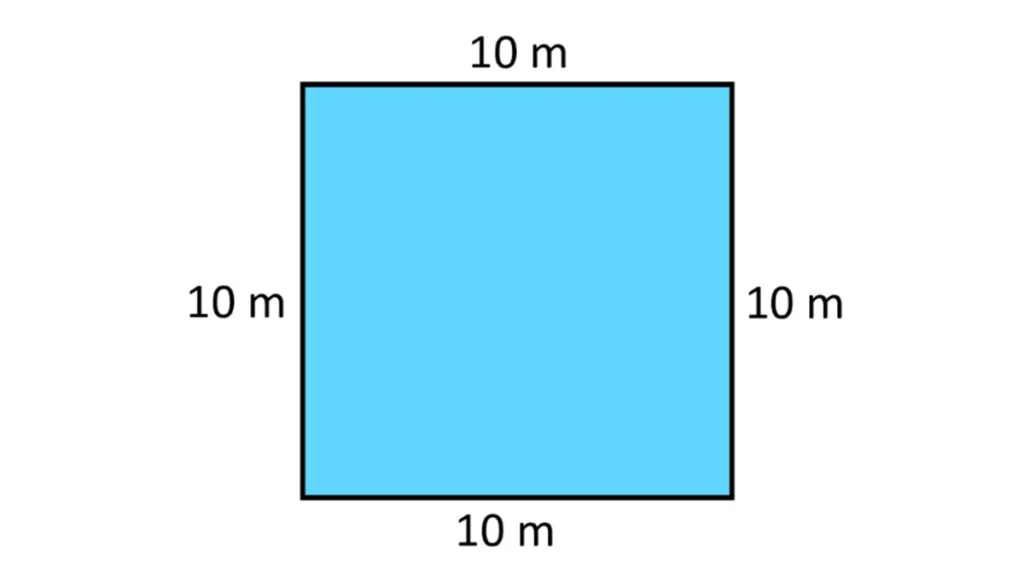
Розглянемо на прикладі, як знайти площу квадрата за цією формулою. Уявімо, що в нас є квадрат зі стороною 4 см. Оскільки в нього всі сторони мають однакову довжину, для обчислення S□ виконуємо такі дії:
- Перемножуємо сторони: S = 4 * 4 = 4².
- Проводимо розрахунок та отримуємо S = 16.
Відповідь: 16 см².

Ще раніще ми писали: Як знайти периметр прямокутника – формула, 5 прикладів задач
За діагоналлю
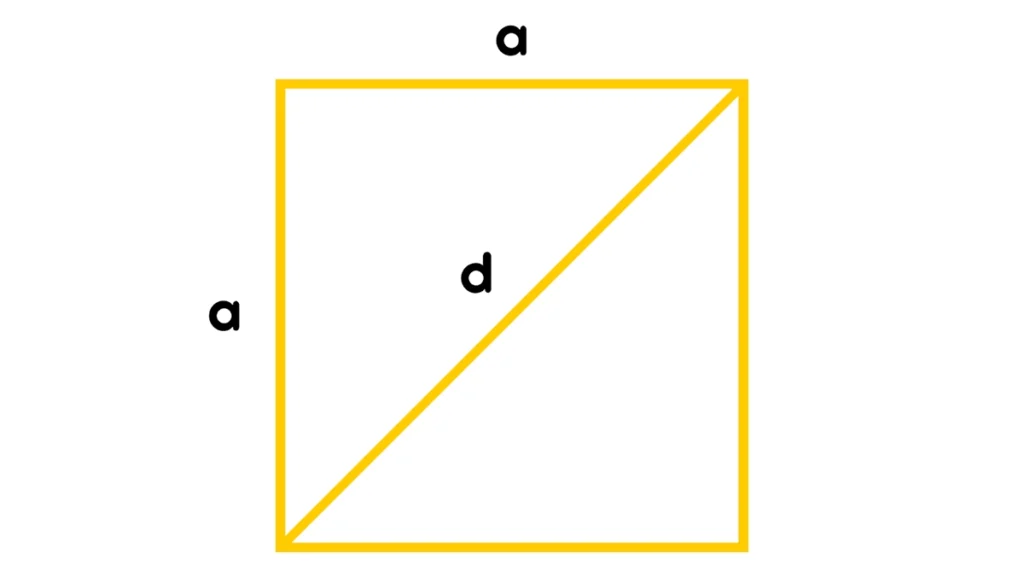
Коли довжина сторони квадратного прямокутника невідома, існують інші способи обчислити його S. Це можна зробити через діагональ d.
Для розрахунку площі в цьому випадку потрібно квадрат множини діагоналі поділити на 2. У вигляді формули це можна записати так: S = d²/2.
Розглянемо використання цієї формули на практиці. Припустимо, що в нас є плоский □ з діагоналлю d, що дорівнює 12 см. Необхідно знайти його S. Виконуємо наступні обчислення:
- Підставляємо відомі дані в формулу: S = 12²/2.
- Проводимо математичні розрахунки: S = 144/2 = 72.
Відповідь: S = 72 см².
Через периметр
У деяких задачах не вказано, скільки дорівнює діагональ чи сторона фігури, але відомий її периметр. В такому випадку не залишається нічого іншого, як знайти S□ за допомогою периметра.
Для початку згадаємо, що периметром називається сума довжин всіх сторін фігури. Оскільки у квадратного прямокутника всі боки рівні, він визначається за формулою P = 4a,
де:
- P – периметр;
- a – довжина сторони.
Завдяки цій формулі можна визначити довжину сторони геометричної фігури: a = P/4.
Після цього для обчислення необхідної величини залишається використати вже відому нам формулу S = a².
Розглянемо, як знайти площу квадрата цим способом на прикладі фігури з периметром 36 см. Для розв’язання задачі виконуємо такі кроки:
- Обчислюємо, скільки дорівнює кожна сторона: a = 36/4 = 9 см.
- Розраховуємо площу: S = 9² = 81 см².
Отже, відповідь – 81 см².
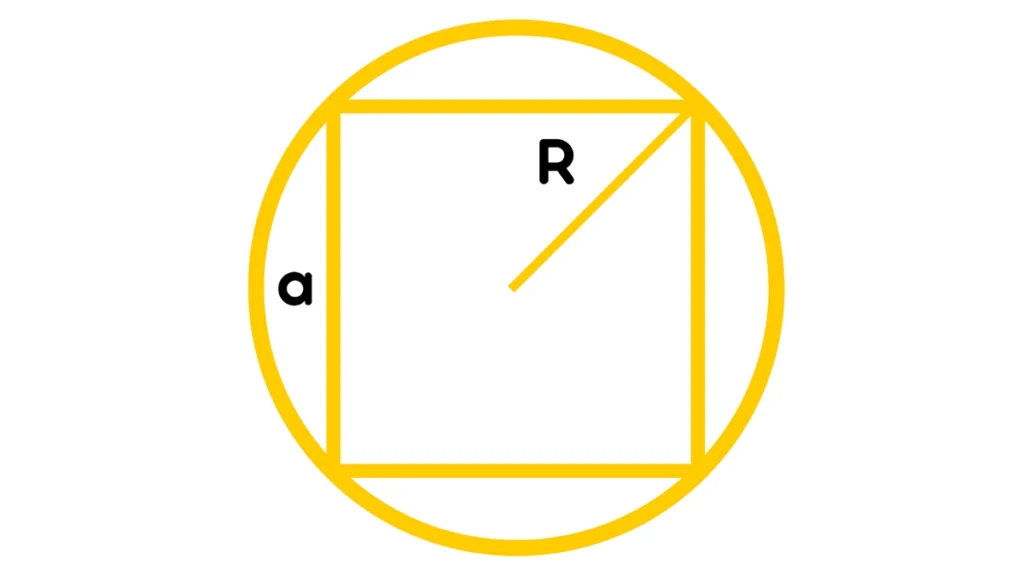
Якщо вписаний в коло
Діагональ квадрата дорівнює діагоналі описаного кола. Оскільки ця фігура – правильний ромб, знайти її площу можна за формулою обчислення S ромба, яка дорівнює половині добутку його діагоналей.
Квадрат має рівні діагоналі, тому формула розрахунку виглядає наступним чином: S = d²/2.
Тепер обчислимо S□, вписаного в коло, якщо відомо, що діагональ кола становить 10 см. Розв’язання:
- Оскільки діагоналі кола та вписаної в нього фігури рівні, використовуємо формулу розрахунку S через діагональ: S = d²/2 = 10²/2.
- Виконуємо обчислення: S = 100/2 = 50 см².
Відповідь: 50 см².
Відео про те, як знайти площу квадрата
Для більш грунтовного вивчення теми пропонуємо вам переглянути відео з YouTube, в якому розповідається про S□, а також наводяться приклади розв’язання задач.
Висновок
Тепер ви знайєте, що площа квадрата може бути знайдена кількома способами, залежно від того, яка інформація відома: довжина сторін, діагональ, периметр або радіус описаного кола. Застосування цих формул дозволяє швидко й точно розрахувати площу фігури для різних практичних завдань. Володіння цими методами є корисним у багатьох сферах, від будівництва до дизайну.
Відповіді на часті питання про те, як знайти площу квадрата
Це розмір поверхні, який займає квадратна форма на площині.
Згідно міжнародної системи вимірювань вона обчислюється в квадратних сантиметрах, метрах, кілометрах тощо.
Для цього потрібно перемножити його довжину на ширину. Оскільки сторони фігури рівні, використовується формула S = a².
Так, для цього потрібно поділити її діагональ, возведену у квадратний ступінь, на два. Отримане число буде необхідним результатом.
Вміння її знаходити може стати в пригоді в багатьох ситуаціях: під час архітектурного планування, будівництва та проведення ремонтних робіт, в комп’ютерній графіці, дизайні, ландшафтному плануванні тощо.